« Fonction convexe » : différence entre les versions
Aucun résumé des modifications |
|||
| Ligne 9 : | Ligne 9 : | ||
== Définition == | == Définition == | ||
Fonction dans laquelle la région au-dessus du graphique est un ensemble convexe. Classiquement, une fonction convexe est en forme de U. Par exemple, les fonctions suivantes sont toutes des fonctions convexes : | Fonction dans laquelle la région au-dessus du graphique est un ensemble convexe. Classiquement, une fonction convexe est en forme de U. Par exemple, les fonctions suivantes sont toutes des fonctions convexes : | ||
| Ligne 28 : | Ligne 26 : | ||
* Régularisation L1 | * Régularisation L1 | ||
* Régularisation L2 | * Régularisation L2 | ||
Version du 3 décembre 2018 à 14:55
Domaine
Définition
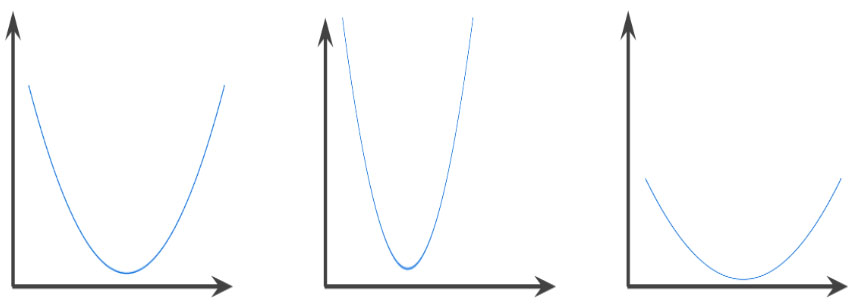
Fonction dans laquelle la région au-dessus du graphique est un ensemble convexe. Classiquement, une fonction convexe est en forme de U. Par exemple, les fonctions suivantes sont toutes des fonctions convexes :
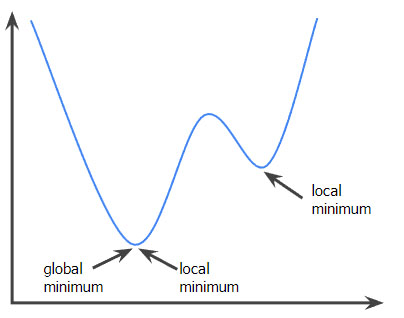
À titre de comparaison, la fonction suivante n'est pas convexe. Notez comment la région au-dessus du graphique diffère d'un ensemble convexe :
Une fonction strictement convexe possède exactement un minimum local, qui est également le minimum global. Les fonctions classiques en U sont des fonctions strictement convexes. Ce n'est pas le cas de certaines fonctions convexes, comme les droites.
De nombreuses fonctions de perte courantes, telles que les fonctions suivantes, sont convexes :
- Perte L2
- Perte logistique
- Régularisation L1
- Régularisation L2
Termes privilégiés
fonction convexe n.f.
Anglais
convex function
Contributeurs: Evan Brach, Jacques Barolet, wiki, Robert Meloche