Fonction convexe

Définition

NOUVEAU et ANCIEN

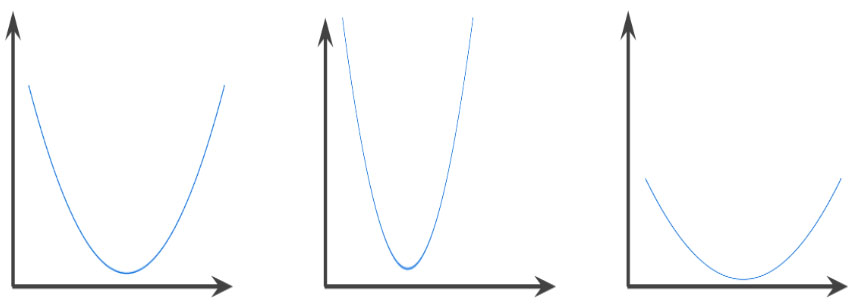
Fonction dans laquelle la région au-dessus du graphique est un ensemble convexe. Classiquement, une fonction convexe est en forme de U. Par exemple, les fonctions suivantes sont toutes des fonctions convexes :

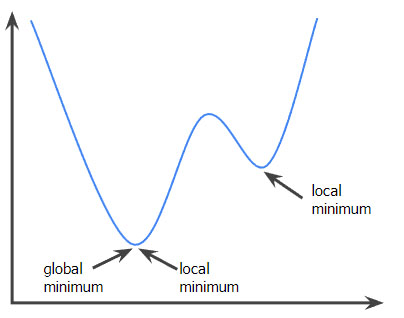
À titre de comparaison, la fonction suivante n'est pas convexe. Notez comment la région au-dessus du graphique diffère d'un ensemble convexe :

Une fonction strictement convexe possède exactement un minimum local, qui est également le minimum global. Les fonctions classiques en U sont des fonctions strictement convexes. Ce n'est pas le cas de certaines fonctions convexes, comme les droites.

De nombreuses fonctions de perte courantes, telles que les fonctions suivantes, sont convexes :

• Perte L2
• Perte logistique
• Régularisation L1
• Régularisation L2

Dans de nombreux cas de descente de gradient, on peut être certain de trouver un point proche du minimum d'une fonction strictement convexe. De même, dans de nombreux cas de descente de gradient stochastique, la probabilité est forte de trouver un point proche du minimum d'une fonction strictement convexe, bien que cela ne soit pas garanti pour autant.

La somme de deux fonctions convexes (par exemple, perte L2 + régularisation L1) est une fonction convexe.

Les modèles profonds ne sont jamais des fonctions convexes. Il est à noter que les algorithmes conçus pour l'optimisation convexe tendent de toute façon à trouver des solutions raisonnablement satisfaisantes pour les réseaux profonds, même s'il n'est pas certain que ces solutions soient des minimums globaux.

Anglais

convex function

Source: Google machine learning glossary