Algorithme EM
Domaine
Apprentissage profond
Définition
Algorithme d'apprentissage non supervisé qui permet de trouver les paramètres du maximum de vraisemblance d'un modèle probabiliste même lorsque ce dernier dépend de variables latentes non observables.
Note :
Cet algorithme itératif comporte deux étapes: 1) Une étape d’évaluation de l’espérance (E) de la fonction de vraisemblance. Cette étape pondère dans quelle mesure chaque donnée contribue à l’estimation de la vraisemblance maximale. 2) Une étape de maximisation (M) de la fonction de vraisemblance trouvée à l’étape E où les paramètres sont ajustés en fonction des données qui ont été repondérées. Les paramètres mis-à-jour à l’étape M sont réinjectés à l’étape E et on itère ainsi jusqu’à la convergence (les paramètres ne changent plus). Puisque l’algorithme EM converge vers un maximum local, pour trouver un maximum global il faut reprendre le calcul un grand nombre de fois avec des paramètres initiaux différents. De nombreuses variantes de l'algorithme initialement proposé par Dempster (1977) ont été élaborées par la suite, donnant ainsi naissance à une famille d'algorithmes. Par exemple, l'algorithme de groupage des K-moyennes peut être considéré comme en faisant partie.
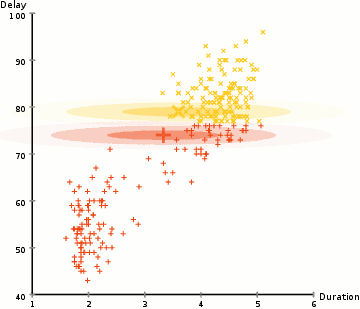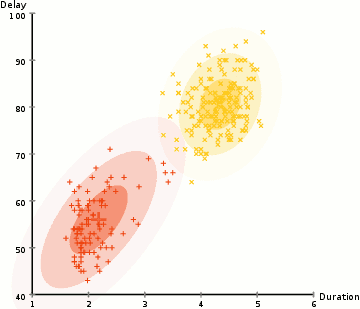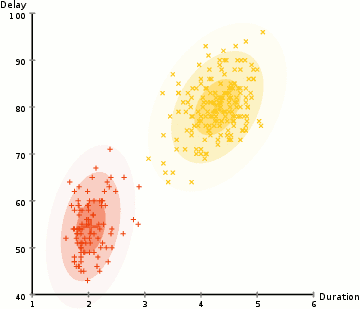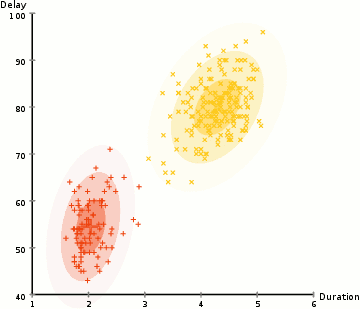
Source : Wikipédia, consulté le 3 juin 2019
[[Source : Li, X. Guttmann, A.; Cipière, S.; Demongeot, J.; JY Boire et L Ouchchane (2014). Utilisation de l’algorithme EM pour estimer les paramètres du chaînage probabiliste d’enregistrements, Revue d'Épidémiologie et de Santé Publique 62(5), page S196.]]
Français
algorithme EM
algorithme espérance-maximisation
Anglais
EM algorithm
Expectation–Maximization algorithm
Contributeurs: Claire Gorjux, Jacques Barolet, Julie Roy, wiki, Robert Meloche
